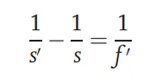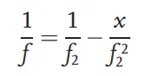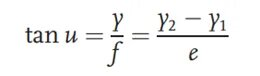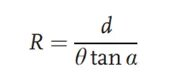1. Жижна даљина оптичких система
Жижна даљина је веома важан показатељ оптичког система, што се тиче концепта жижне даљине, мање-више имамо разумевање, па ћемо га овде прегледати.
Жижна даљина оптичког система, дефинисана као растојање од оптичког центра оптичког система до фокуса снопа када пада паралелна светлост, је мера концентрације или дивергенције светлости у оптичком систему. Користимо следећи дијаграм да илуструјемо овај концепт.
На горњој слици, паралелни сноп који пада са левог краја, након проласка кроз оптички систем, конвергира ка фокусу слике F', обрнута линија продужетка конвергентног зрака сече се са одговарајућом линијом продужетка упадног паралелног зрака у тачки, а површина која пролази ову тачку и нормална је на оптичку осу назива се задња главна раван, задња главна раван сече се са оптичком осом у тачки P2, која се назива главна тачка (или оптички центар), растојање између главне тачке и фокуса слике, то је оно што обично називамо жижном даљином, пуни назив је ефективна жижна даљина слике.
Такође се са слике може видети да се растојање од последње површине оптичког система до фокалне тачке F' слике назива задња жижна даљина (ЗЖД). Сходно томе, ако паралелни сноп пада са десне стране, постоје и концепти ефективне жижне даљине и предње жижне даљине (ПЖД).
2. Методе тестирања жижне даљине
У пракси постоји много метода које се могу користити за испитивање жижне даљине оптичких система. На основу различитих принципа, методе испитивања жижне даљине могу се поделити у три категорије. Прва категорија се заснива на положају равни слике, друга категорија користи однос између увећања и жижне даљине да би добила вредност жижне даљине, а трећа категорија користи закривљеност таласног фронта конвергентног светлосног снопа да би добила вредност жижне даљине.
У овом одељку ћемо представити уобичајене методе за испитивање жижне даљине оптичких система:
2.1CМетода олиматора
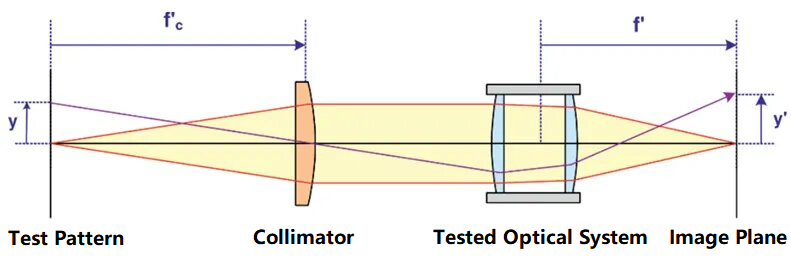
Принцип коришћења колиматора за испитивање жижне даљине оптичког система је приказан на дијаграму испод:
На слици је тестни образац постављен у фокус колиматора. Висина y тестног обрасца и жижна даљина fc' колиматора су познати. Након што се паралелни сноп који емитује колиматор конвергира тестираним оптичким системом и слика на равни слике, жижна даљина оптичког система може се израчунати на основу висине y' тестног обрасца на равни слике. Жижна даљина тестираног оптичког система може се израчунати помоћу следеће формуле:
2.2 ГаусоваMметод
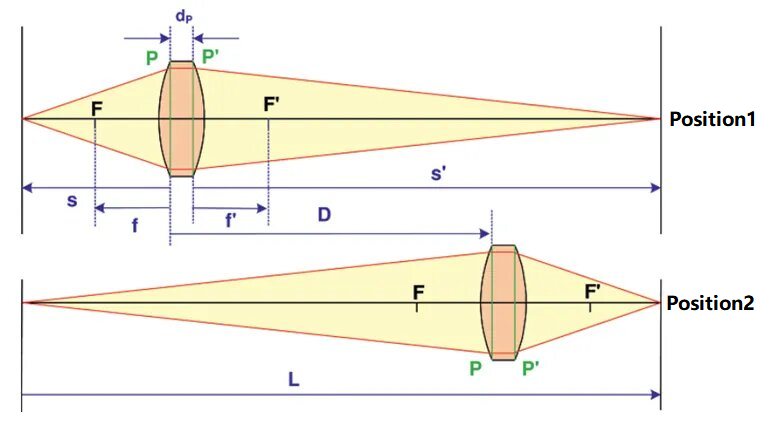
Шематски приказ Гаусове методе за тестирање жижне даљине оптичког система је приказан испод:
На слици су предња и задња главна раван тестираног оптичког система представљене као P и P' респективно, а растојање између две главне равни је dPУ овој методи, вредност dPсе сматра познатим или је његова вредност мала и може се занемарити. Објекат и пријемни екран се постављају на леви и десни крај, а растојање између њих се бележи као L, где L треба да буде веће од 4 пута веће од жижне даљине система који се тестира. Систем који се тестира може се поставити у два положаја, означена као положај 1 и положај 2, респективно. Објекат са леве стране се може јасно видети на пријемном екрану. Растојање између ове две локације (означене као D) може се измерити. Према конјугованој вези, можемо добити:
На ове две позиције, удаљености објеката се бележе као s1 и s2 респективно, тада је s2 - s1 = D. Извођењем формуле можемо добити жижну даљину оптичког система као што је приказано испод:
2.3Лензометар
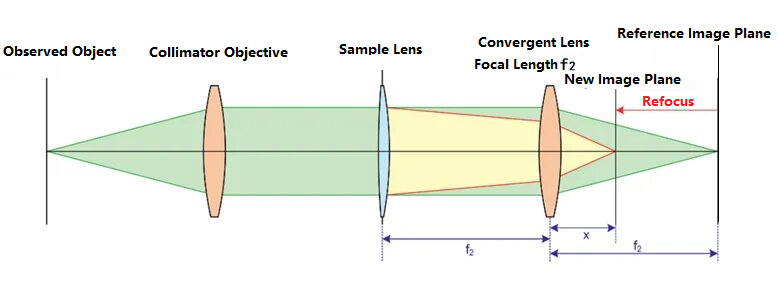
Ленсометар је веома погодан за испитивање оптичких система са великом жижном даљином. Његова шематска слика је следећа:
Прво, сочиво које се тестира није постављено на оптичку путању. Посматрана мета са леве стране пролази кроз колиматорно сочиво и постаје паралелна светлост. Паралелна светлост се конвергира помоћу конвергентног сочива са жижном даљином f.2и формира јасну слику на референтној равни слике. Након што је оптичка путања калибрисана, сочиво које се тестира се поставља на оптичку путању, а растојање између сочива које се тестира и конвергентног сочива је f2Као резултат тога, услед деловања тестираног сочива, светлосни сноп ће бити рефокусиран, што ће изазвати померање положаја равни слике, што ће резултирати јасном сликом на положају нове равни слике на дијаграму. Растојање између нове равни слике и конвергентног сочива означено је као x. На основу односа објекат-слика, жижна даљина тестираног сочива може се закључити као:
У пракси, лензометар се широко користи у мерењу горње жижне даљине форама наочара и има предности једноставног рада и поуздане прецизности.
2.4 АбеRефрактометар
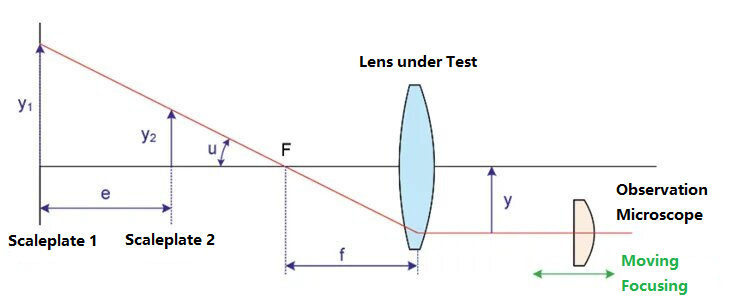
Абеов рефрактометар је још једна метода за испитивање жижне даљине оптичких система. Његова шематска слика је следећа:
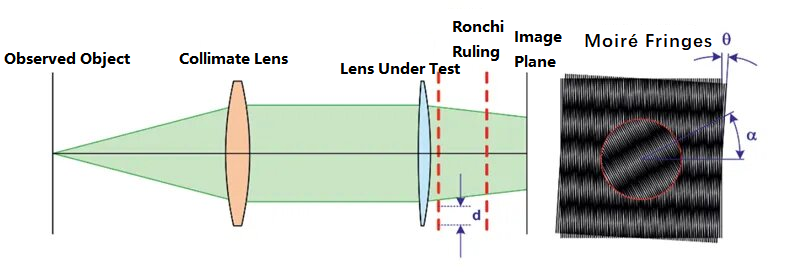
Поставите два лењира различитих висина на страну објекта на површини тестираног сочива, наиме скалу 1 и скалу 2. Одговарајуће висине скала су y1 и y2. Растојање између две скале је e, а угао између горње линије лењира и оптичке осе је u. Скала се снима тестираним сочивом са жижном даљином f. Микроскоп је постављен на крај површине слике. Померањем положаја микроскопа проналазе се горње слике две скале. У овом тренутку, растојање између микроскопа и оптичке осе означено је као y. Према односу објекта и слике, можемо добити жижну даљину као:
2.5 Моаре дефлектометријаМетод
Метода Моаре дефлектометрије користиће два сета Ронкијевих пруга у паралелним светлосним сноповима. Ронкијеве пруге су решеткасти узорак металног хромског филма нанетог на стакленој подлози, који се обично користи за тестирање перформанси оптичких система. Метода користи промену Моареових пруга које формирају две решетке за тестирање жижне даљине оптичког система. Шематски дијаграм принципа је следећи:
На горњој слици, посматрани објекат, након проласка кроз колиматор, постаје паралелни сноп. У оптичкој путањи, без претходног додавања тестираног сочива, паралелни сноп пролази кроз две решетке са углом померања θ и размаком решетки d, формирајући скуп Моареових пруга на равни слике. Затим се тестирано сочиво поставља у оптичку путању. Оригинална колимирана светлост, након преламања од стране сочива, произвешће одређену жижну даљину. Полупречник закривљености светлосног снопа може се добити из следеће формуле:
Обично се сочиво које се тестира поставља веома близу прве решетке, тако да вредност R у горњој формули одговара жижној даљини сочива. Предност ове методе је што може да тестира жижну даљину система позитивне и негативне жижне даљине.
2.6 ОптичкиFИберAаутоколимацијаMметод
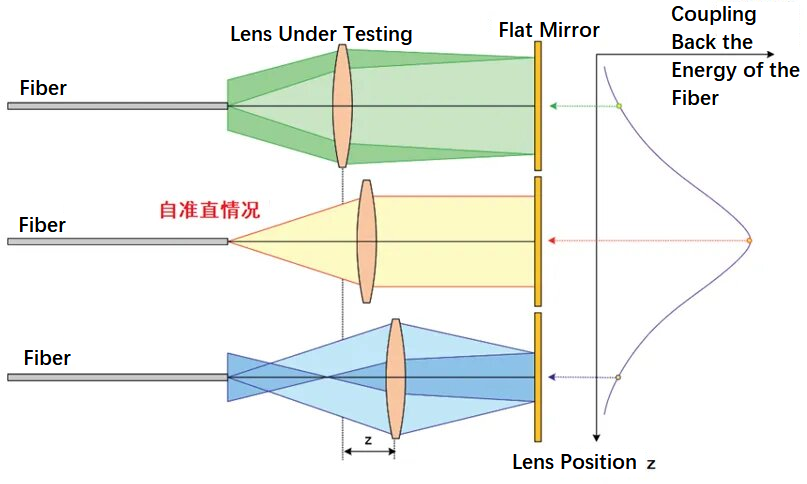
Принцип коришћења методе аутоколимације оптичких влакана за испитивање жижне даљине сочива приказан је на слици испод. Користи оптичка влакна за емитовање дивергентног снопа који пролази кроз сочиво које се тестира, а затим на равно огледало. Три оптичке путање на слици представљају услове оптичког влакна унутар фокуса, унутар фокуса и ван фокуса, респективно. Померањем положаја сочива које се тестира напред-назад, можете пронаћи положај главе влакна у фокусу. У овом тренутку, сноп се самоколимира, и након рефлексије од равног огледала, већина енергије ће се вратити у положај главе влакна. Метода је једноставна у принципу и лака за имплементацију.
3. Закључак
Жижна даљина је важан параметар оптичког система. У овом чланку детаљно описујемо концепт жижне даљине оптичког система и методе његовог тестирања. У комбинацији са шематским дијаграмом, објашњавамо дефиницију жижне даљине, укључујући концепте жижне даљине на страни слике, жижне даљине на страни објекта и жижне даљине од напред до назад. У пракси постоји много метода за тестирање жижне даљине оптичког система. Овај чланак представља принципе тестирања колиматорске методе, Гаусове методе, методе мерења жижне даљине, Абеове методе мерења жижне даљине, методе Моареовог скретања и методе аутоколимације оптичких влакана. Верујем да ћете читањем овог чланка боље разумети параметре жижне даљине у оптичким системима.
Време објаве: 09.08.2024.